Faulty Combination Lock
19 Apr 2020 - Drew CumminsThis was a deceptive little puzzle from the National Museum of Mathematics’ Mind-Benders for the Quarantined!, which ended up being a real slog for me to solve.
Here’s the problem statement, in all its cunning simplicity:
A combination lock with three dials, each numbered 1 through 8, is defective in that you only need to get two of the numbers right to open the lock. (For example, suppose the true combination is 4-2-7. Then 4-2-7 would open the lock, but so would 4-2-5, 4-2-2, 8-2-7, or 4-6-7. But not 2-4-7.)
What is the minimum number of (three-number) combinations you need to try in order to be sure of opening the lock?
A Quick Glossary
It’s going to be a lot clearer if we explicitly define some terminology, primarily for situational disambiguation, but also because combination means something specific in mathematics that is unfortunately at odds with how it’s used w.r.t. locks.
| permutation | a valid setting of the lock’s dials, e.g. 3-8-1 |
| configuration | the permutation the lock-maker set it to |
| guess | a permutation we’re hoping unlocks the lock |
| cover | a configuration is covered if a guess would unlock it |
Done and Dumb and Confident
At first glance, this seems simple: if one of the dials doesn’t matter, we just have to try all possible permutations of 2 dials for a total of guesses (2 dials, 8 numbers each), after which we can be certain to have unlocked the damned thing.
But this isn’t actually the best we can do. Let’s first consider the much smaller case of 3 dials numbered 1 through 2 instead, which at total permutations is much easier to investigate. According to that initial premise, we would expect to find guesses necessary to guarantee solving such a lock, but it turns out we can do it in just two.
It’s easy to see how this is possible if we try the guesses and :
These are the only possible permutations of such a lock, and hopefully it’s easy to see via the coloring that together, and cover every possible configuration.
Combinatoric Approach
Let’s try to reason a bit about this by considering how many configurations are covered by a guess. There are 3 pairs of dials: (1,2), (1,3) and (2,3). So a guess will cover all configurations that share any of those pairs, since we only need 2 dials to match. So for each pair, we cover as many permutations as there are settings of the remaining dial—in this toy case 2, in the actual puzzle, 8. So that gives us 3 pairs times 2 settings of the remaining dial, minus the 2 extra times we counted our guess permutation: , and for the actual puzzle.
This means each guess covers configurations, where is how many numbers there are per dial. Since we’ve already shown 2 guesses in our toy case that cover all configurations (read: it’s possible to do it in 2), and we know each guess covers 4 configurations and 4 is less than the 8 total permutations (read: it’s impossible to do in less than 2), this proves 2 is the solution to the toy puzzle.
Unfortunately, things don’t work out so well for the actual puzzle—22 doesn’t divide the total permutations. From this we can deduce that some of our guesses must cover the same configurations, and so we know from this point out that the solution, at least from a counting-down combinatoric approach, must be a far hairier affair. We can, however, give a lower bound to the answer: .
I toiled with the way guesses overlapped, but didn’t ever make any meaningful progress. You can’t brute force it, because even with our lower bound, there are 98,173,718,189,790,929,581,466,857,579,452,509,896,000 unique subsets of 24 guesses. That number is probably LaRgEr ThAn tHe NuMbEr oF aToMs iN ThE uNiVErSe or something, but I think everyone’s tired of hearing that sort of thing.
Geometric Approach
If we instead think of each permutation as a point in space (the first dial moves us along the x-axis, the second dial along the y-axis and the third dial along the z-axis), we end up with an cube with some neat properties.
Each guess is now a point, and each covered configuration is collinear with that guess, and parallel to the x, y or z axes. Another way of thinking about it is that a guess sits at the intersection of 3 lines—each of those lines represents a broken dial: if we have dial 1 (x-axis) and 2 (y-axis) correct, then all configurations with those (x,y) coordinates are covered, regardless of dial 3 (z-axis). This gives us some spatial intuition for how to construct our list of guesses.
This is probably easier to just look at:
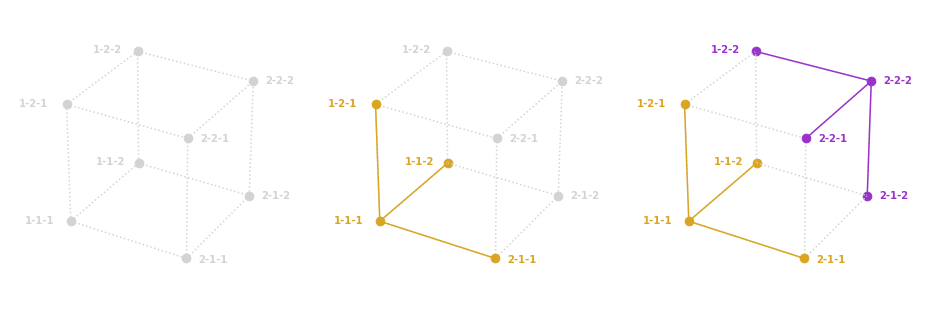
First we’ve plotted all possible permutations of our toy lock, then in the middle diagram, we guess and color each configuration this guess covers, and then finally guess , at which point it should be apparent we’ve covered all possible configurations.
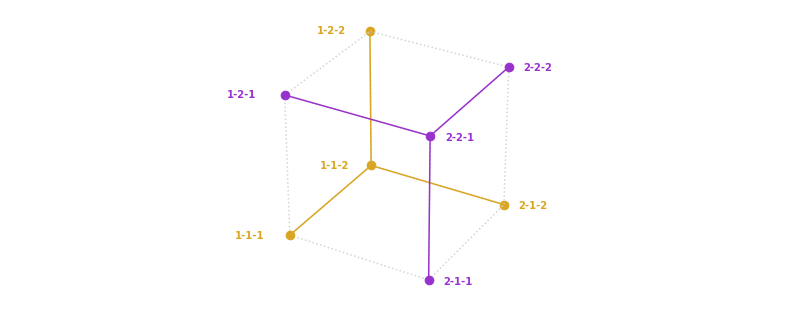
It might not have been apparent before, but now we can easily find other pairs of guesses that also unlock our toy lock, e.g. and :
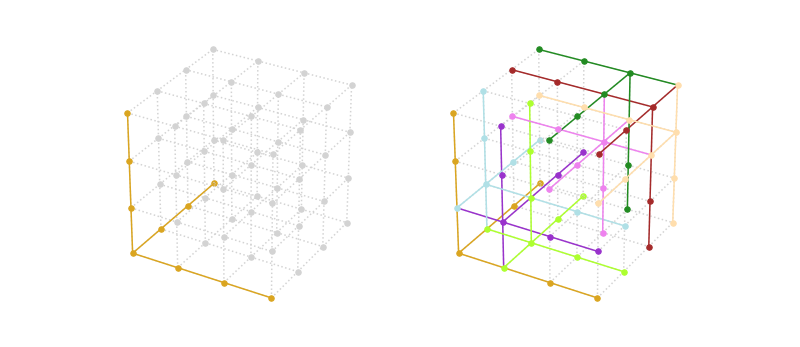
Unfortunately even this approach becomes on its own quickly unwieldy for larger . Look at our first guess and a completed version for :
It’s just not immediately apparent (or wasn’t, to me) how we minimize overlap in our guesses. Let’s first see if we can figure out how many guesses we need, then we’ll figure out which guesses. If we take a slightly different tack and constrain ourselves to a single (x,y) plane in space at a time, a few things jump out:
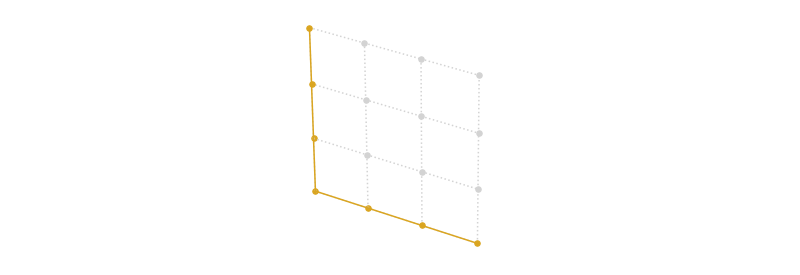
First, this initial guess will cover configurations, for as in the diagram. If this was the only guess we ever made on this plane, what is the minimum number of guesses we’d have to make on other planes to cover each remaining configuration here? , because a guess on a different plane can only cover a single configuration on this plane, and the above diagram has currently uncovered configurations. Clearly each plane benefits more from a configuration belonging to it, rather than another plane.
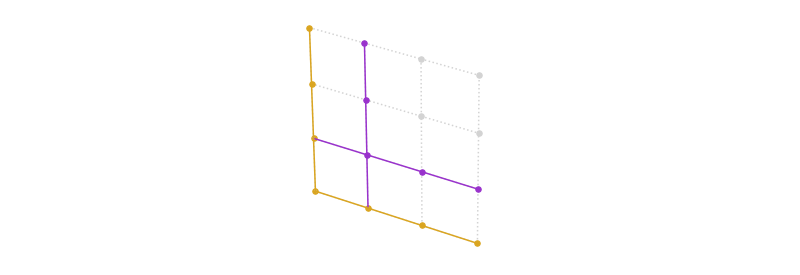
Next, our second guess covers at most ( in this case) new configurations. So it looks like our th guess covers new configurations on the plane, and with a little work we can see that after the th guess on the plane, we’ve covered of its configurations.
Since each plane benefits most from a configuration belonging to it, the optimal strategy is to evenly distribute guesses across all planes. But how many extraplanar guesses should we rely on? Looking back to our toy case, we see that we’re relying on guesses from half of the planes. Let’s assume this is correct for now.
We can put all of this together into an equation:
\[ {2nm - m^2} + \frac{nm}{2} = n^2 \]
This equation basically says “the number of configurations we cover with guesses on this plane, plus the number of guesses per plane on half the planes is equal to the total number of configurations on this plane”. Solving this gives us , which fits our toy case.
Now let’s choose our guesses as we continue with this assumption (it’s easier to see why it’s right after doing so). We’ll stick with the case for now. We know we want to make guesses per plane, and that each plane should have configurations covered by other planes.

If we look again at this diagram, we see it fits this description. We know that those 4 configurations in the top right must come from half of the planes (), so what do those planes look like?
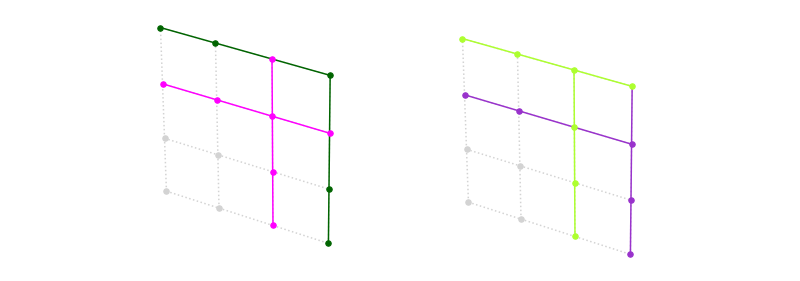
The final piece of the puzzle is that of the configurations to cover on the initial plane, each row and each column must be uniquely covered. This is easier to see in a different diagram, where we represent which plane is doing the covering by symbol instead:

The pattern is repeated in each catacorner quadrant, so we can actually write our list of guesses as a single one of those quadrants, which is done below for the original problem:
